Tarjan 求割点和割边

Tarjan 可以在 $O(n)$ 的时间复杂度内求出一个无向图中的割点、割边。

求割点

在 Tarjan 的过程中，需要对每个节点 $u$ 维护以下变量：

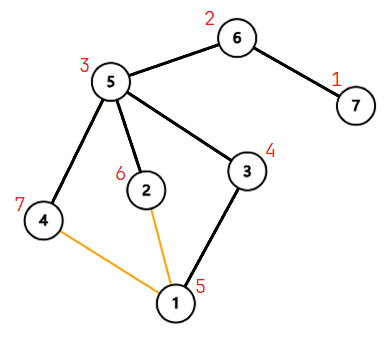
黑色为树边，橙色为非树边；红字为 $\text{dfn}$

• DFS 序 $\text{dfn}_u$。$\text{dfn}$ 是前序更新的，一旦我们进入一个节点，就更新它的 $\text{dfn}$。
• 从 $u$ 出发、可以经过树边和非树边、不经过 $u$ 的父节点能到达的、DFS 序最小的节点的 DFS 序 $\text{low}_u$。例如上图中 $\text{low}_2=4$（$2\to1\to3$，$\text{dfn}_3=4$）。$\text{low}$ 是后序更新的，我们从 $u$ 的子节点退出后，利用其信息更新 $\text{low}_u$。（注意要把 $\text{low}_u$ 初始化为 $\text{dfn}_u$）具体来说，当我们 DFS 到一条边 $(u,v)$ 时：

  • 如果 $v$ 未访问过，说明它是子节点，于是递归搜索 $v$。回溯时，$\text{low}_u\gets\min\{\text{low}_u,\text{low}_v\}$。这是因为：子节点的 $\text{low}$ 不会“回头”，这样连下去的节点不会经过 $u$ 的父节点。于是子节点能连到的 $\text{low}$，$u$ 当然也能连到。

  • 如果 $v$ 访问过了，说明它不是子节点。$\text{low}_u\gets\min\{\text{low}_u,\text{dfn}_v\}$。

我们判断某个点是否是割点的根据是：对于某个顶点 $u$，如果存在一个儿子 $v$，使得 $\text{low}_v \ge \text{dfn}_u$，即不能回到祖先，那么 $u$ 点为割点。

例如上图中点 $5$（$\text{dfn}_5=3$），容易看出其子树中所有节点的 $\text{low}$ 都 $\gt3$，所以可以判断它是割点。

但是这个判据不适用于搜索起点 $s$ 就是割点的情况。请看下面的图（从 $3$ 开始搜索）：

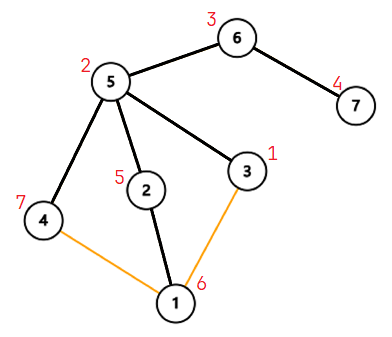
我们发现，如果 $s$ 不是割点，那么能从 $s$ 的任意一个直接儿子出发，到达图中所有节点。所以，$s$ 只会“向下搜”一次。反之，如果 $s$“向下搜”了 $\ge2$ 次，说明 $s$ 就是割点。

注意

“不适用”的意思是：$u$ 为搜索起点时，即使满足判据也不是割点，需要另外的判据。

总结 & 编码

对于节点 $u$，其是割点，当且仅当：

• $u$ 不是搜索起点，且存在 $u$ 的一个儿子 $v$，使得 $\text{low}_v\ge\text{dfn}_u$。
• $u$ 是搜索起点，且 $u$ 在搜索树上只有一个儿子。

编码如下，请重点关注更新 low 的两行：

// 标记割点并统计割点数量
void tarjan(int rt, int fa = 0) {
    node[rt].low = node[rt].dfn = node[fa].dfn + 1;
    int son = 0;
    for (int e = node[rt].head; e; e = edge[e].next) {
        int v = edge[e].to;
        if (!node[v].dfn) { // 没搜到过，是儿子
            son++;
            tarjan(v, rt);
            node[rt].low = min(node[rt].low, node[v].low);
            if (fa != 0 && !node[rt].isCut && node[v].low >= node[rt].dfn) {
                node[rt].isCut = true, cnt++;
            }
        } else {
            node[rt].low = min(node[rt].low, node[v].dfn);
        }
    }
    if (fa == 0 && !node[rt].isCut && son > 1) {
        node[rt].isCut = true, cnt++;
    }
}

例题

• P3388 【模板】割点（割顶）

求割边

方法和求割点非常类似。边 $(u,v)$ 是割边，当且仅当 $\text{low}_v\gt\text{dfn}_u$。（不需要考虑 $u$ 是根节点的问题）注意这里不能取等。

参考

• 割点和桥 - OI Wiki