Tarjan 算法

我也不知道为什么要把这几个算法写在同一篇文章里面。

Tarjan 总之是一种 DFS 算法。下面的 $n$ 都是节点数， $m$ 是边数。而所谓 tarjan() 其实就是 dfs()。

最近公共祖先（LCA）

Tarjan 算法可以在 $\approx O(n+m)$ 的时间复杂度下，离线地处理 LCA 查询。

过程：

创建一个并查集。注意这个并查集只能用路径压缩来优化，不能用按秩合并。而且稍后我们会手动合并，因为要严格控制节点的上下级关系。
从根节点开始 tarjan()。对于我们搜索到的每个节点 $u$ ，执行以下操作：
- 递归搜索所有没访问过的、与 $u$ 相连的节点。（先标记 vis[] 再进入 tarjan()）
- 回溯的时候，我们将正在遍历的子节点 $v$ 的父亲合并到 $u$ 。（fa[v] = u）
- 所有子节点搜索完成后，检索涉及 $u$ 的询问。如果存在询问 $\text{LCA}(u,v)$ ，则检查是否已访问 $v$ （if(vis[v])）。如果已访问 $v$ ，记录 $\text{LCA}(u,v)=\text{find}(v)$ 。

注意！vis[] 是在进入 tarjan() 之前设置的，而 fa[] 是退出 tarjan() 后设置的，有区别！

原理分析：

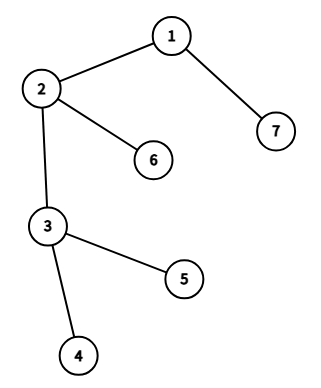
请看上面的树（编号就是 DFS 序），假设我们现在遍历到了 $2$ ，当我们完成子树的遍历时，开始处理查询：

$3,4,5,6$ 已经搜索过了，所以它们都在并查集中，且终极祖先都是当前节点 $2$ 。
假如我们现在要处理查询 $\text{LCA}(2,3)$ ，显然 vis[3] == true，所以 $\text{LCA}(2,3)=\text{find}(3)=2$ 。

再比如，我们什么时候会处理查询 $\text{LCA}(3,6)$ 呢？

总结一下 vis[] 和并查集的作用：

vis[v] 维护的是：节点 $v$ 是否已被访问过。如果被访问过，说明节点 $v$ 和当前节点 $u$ 的 $\text{LCA}$ 一定已经被搜索了。你可能会问，有可能 $v$ 和当前节点的 $\text{LCA}$ 已经被访问过了，但是 vis[v] == false 啊。不要紧，之后我们肯定会进入 $v$ 节点处理查询，这样就转化为第一种情况了。
而 $\text{find}(v)$ 维护的是：节点 $v$ 和当前节点 $u$ 的那个 $\text{LCA}$ 是谁。

Tarjan 算法可以在 $O(n+m)$ 的时间复杂度下求出一个图的强连通分量。

Tarjan 求 SCC 的算法，老师说是目前能接触到的最复杂的算法。

这种算法在一篇获图灵奖的论文中发表，其原理非常复杂。

实际操作中当成黑箱来用就可以了。

Tarjan 算法中需要额外给图中每个节点 $u$ 维护以下变量：

$\text{dfn}_u$ ：做 DFS 时 $u$ 被访问的次序，即 DFS 序。
$\text{low}_u$ ：在 $u$ 的子树中，能够回溯到的、最早的已经在栈里的节点。（这个栈在下文解释）设以 $u$ 为根的子树为 $\text{Subtree}_u$ ，则 $\text{low}_u$ 定义为以下节点的 $\text{dfn}$ 的最小值：
- $\text{Subtree}_u$ 中的节点。
- 从 $\text{Subtree}_u$ 通过一条不在搜索树上的边能到达的节点。

同时我们还要维护一个栈 $\text{stk}[]$ （用数组实现）。实际写代码的时候，为了方便知道一个节点是否在栈中，我们还要维护一个数组 $\text{inStk}[]$ 。

下面讲解如何维护 $\text{low}_u$ （难点）：