绪论
圆锥曲线,指的是用平面截取圆锥(严格来说是二次锥面)得到的曲线(Conic Sections)。从解析几何的角度讲,这样得到的曲线都可以用二元二次方程来表示,因而又称二次曲线(Quadratic Curves)。出于习惯,这里还是称为 “圆锥曲线”。
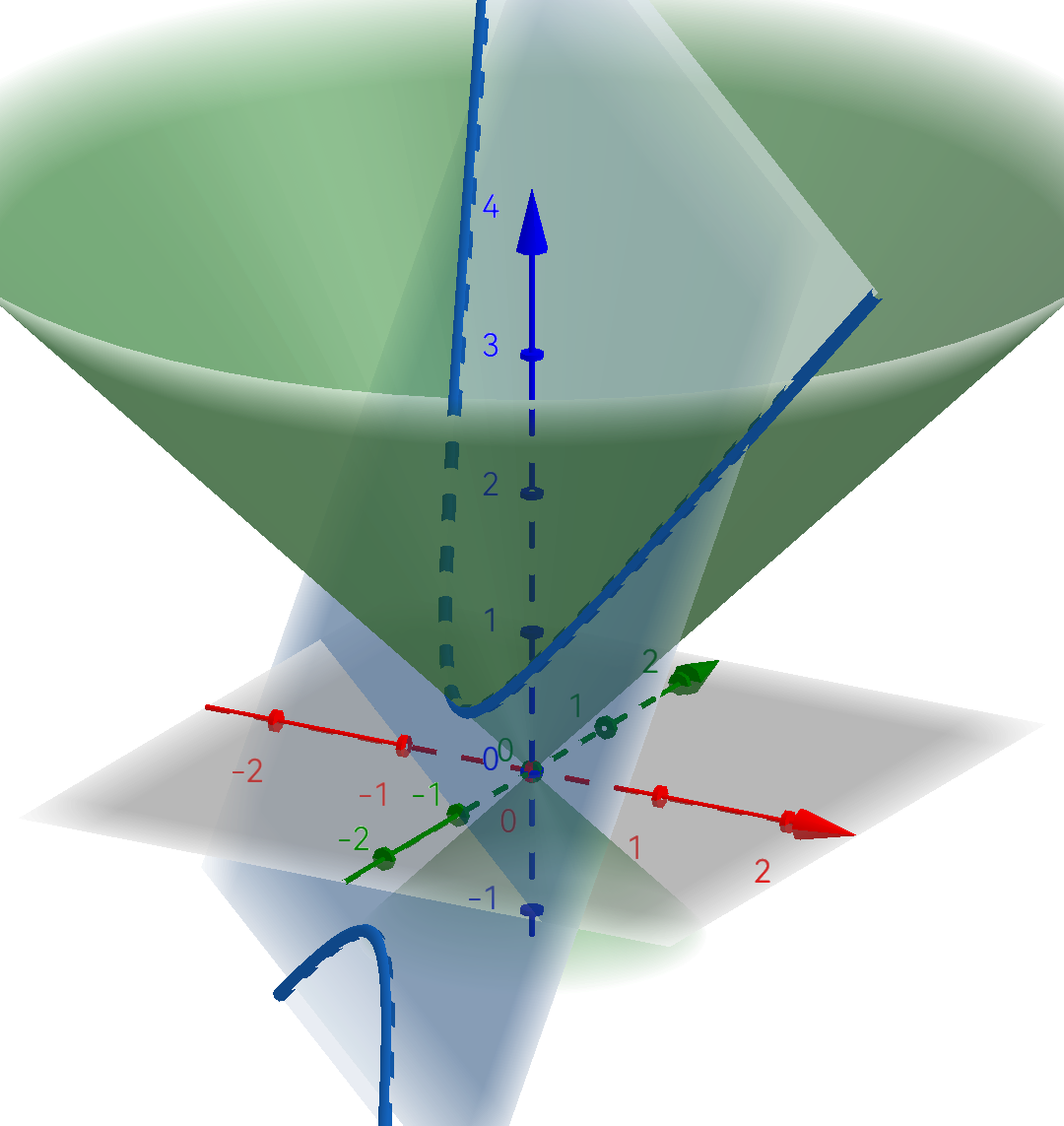
由平面截锥面得到的双曲线
圆锥曲线有下面几种(不包含退化的):
| 名称 | 标准方程 | 离心率 |
|---|---|---|
| (圆) | ||
| 椭圆 | ||
| 抛物线 | ||
| 双曲线 |
高中阶段,圆锥曲线类题目重点研究椭圆、双曲线、抛物线,而圆不在此范畴。虽然这些曲线的方程不尽相同,但是在做题方法、二级结论上很相似。
符号
圆锥曲线中的一些数学符号是通用的:
-
,即离心率。
-
,即焦点到准线的长度。