跳到主要内容

椭圆：二级结论

椭圆的二级结论。多用于小题，也可以为大题提供思路。

由第一定义得出​

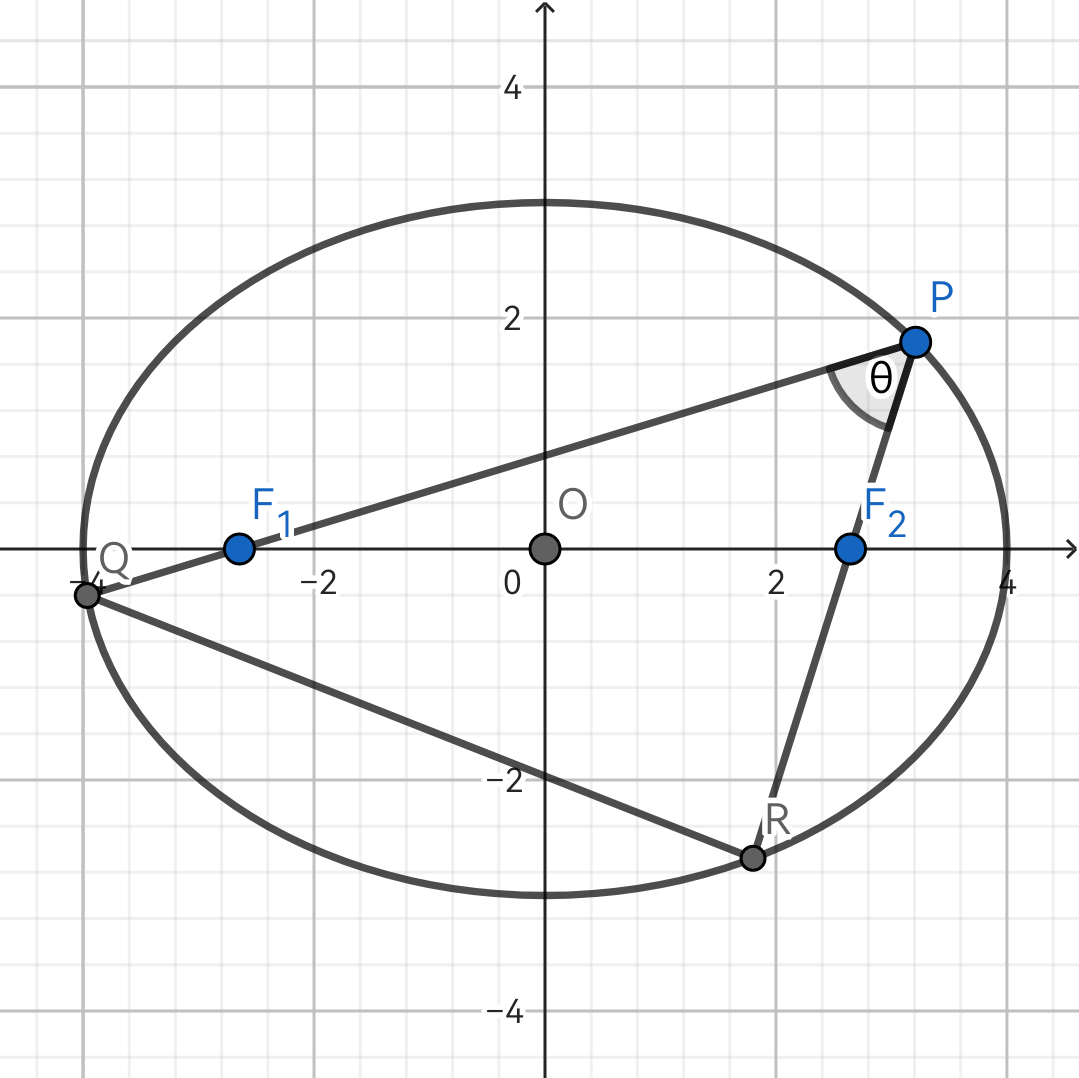
Fig. 1(a)\text{Fig. 1(a)}

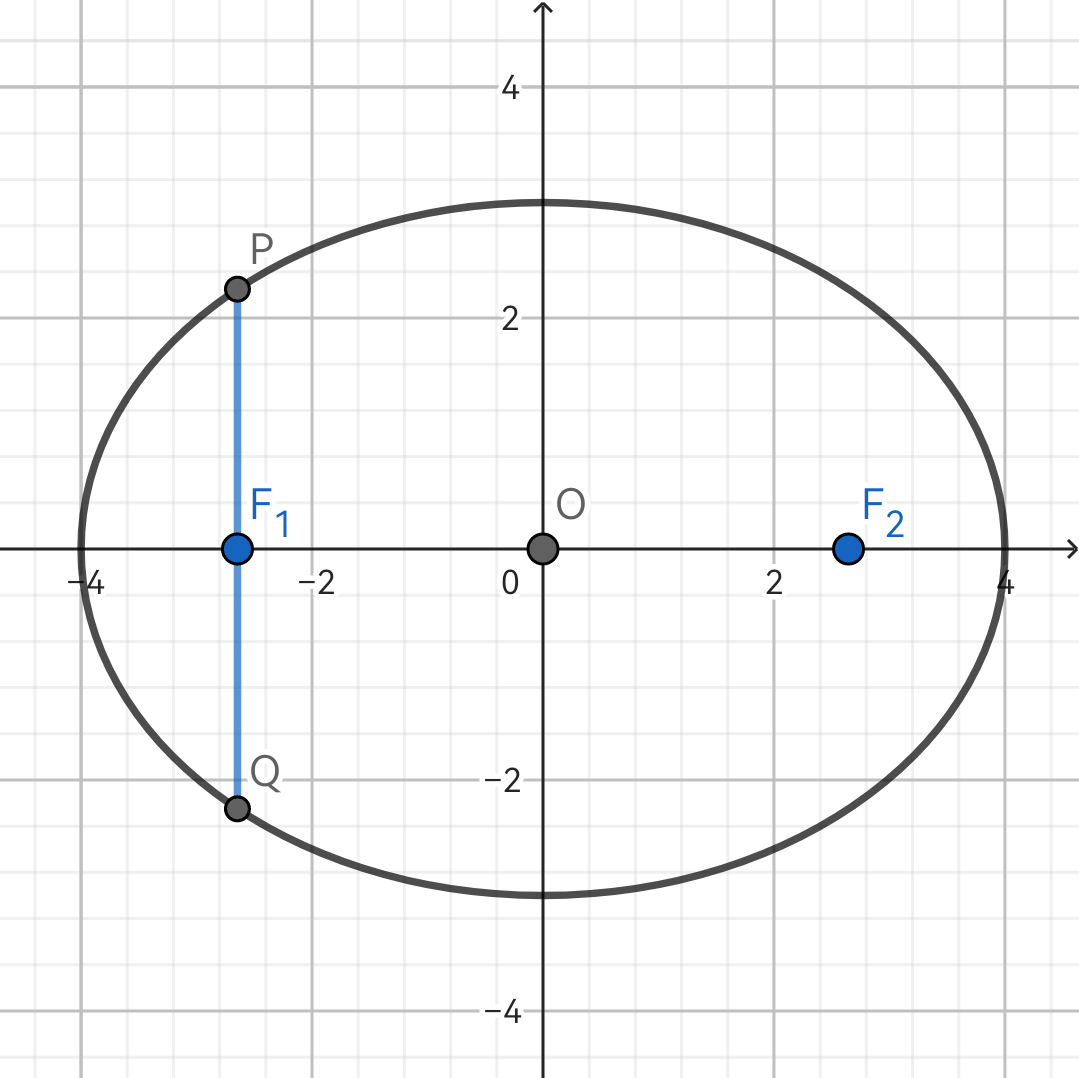
Fig. 1(b)\text{Fig. 1(b)}

1.1(a)  \bold{1.1}\text{(a)}\space\space 过焦点 F1F_1 的直线与椭圆交于 P,QP,Q 两点，连接 P,QP,Q 与另一焦点 F2F_2，则 △PQF2\triangle PQF_2 的周长为 4a.4a.

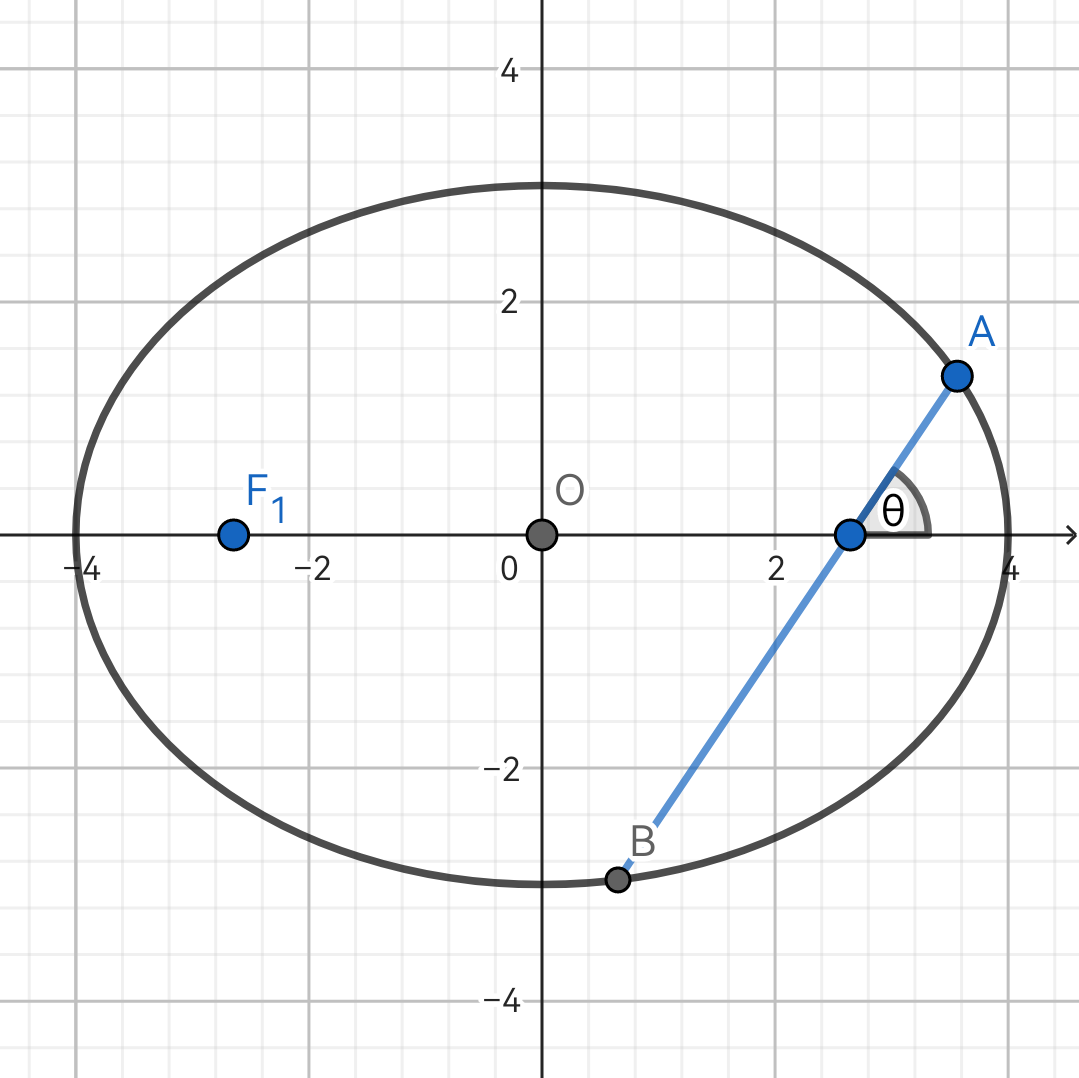
1.2(a)  \bold{1.2}\text{(a)}\space\space PP 为椭圆上一点，连接 PF1,PF2PF_1,PF_2，∠F1PF2=θ\angle F_1PF_2=\theta，则 S△PF1F2=b2tan⁡θ2.S_{\triangle PF_1F_2}=b^2\tan\cfrac{\theta}{2}.

1.3(b)  \bold{1.3}\text{(b)}\space\space 过焦点作 PQ⊥xPQ\perp x 轴，交椭圆于 P,QP,Q 两点，则 PQPQ 称为通径。右图中有 P(−c,−b2a),Q(−c,b2a)P(-c,-\cfrac{b^2}{a}),Q(-c,\cfrac{b^2}{a})，PQ=2b2a.PQ=\cfrac{2b^2}{a}.

由第二定义得出​

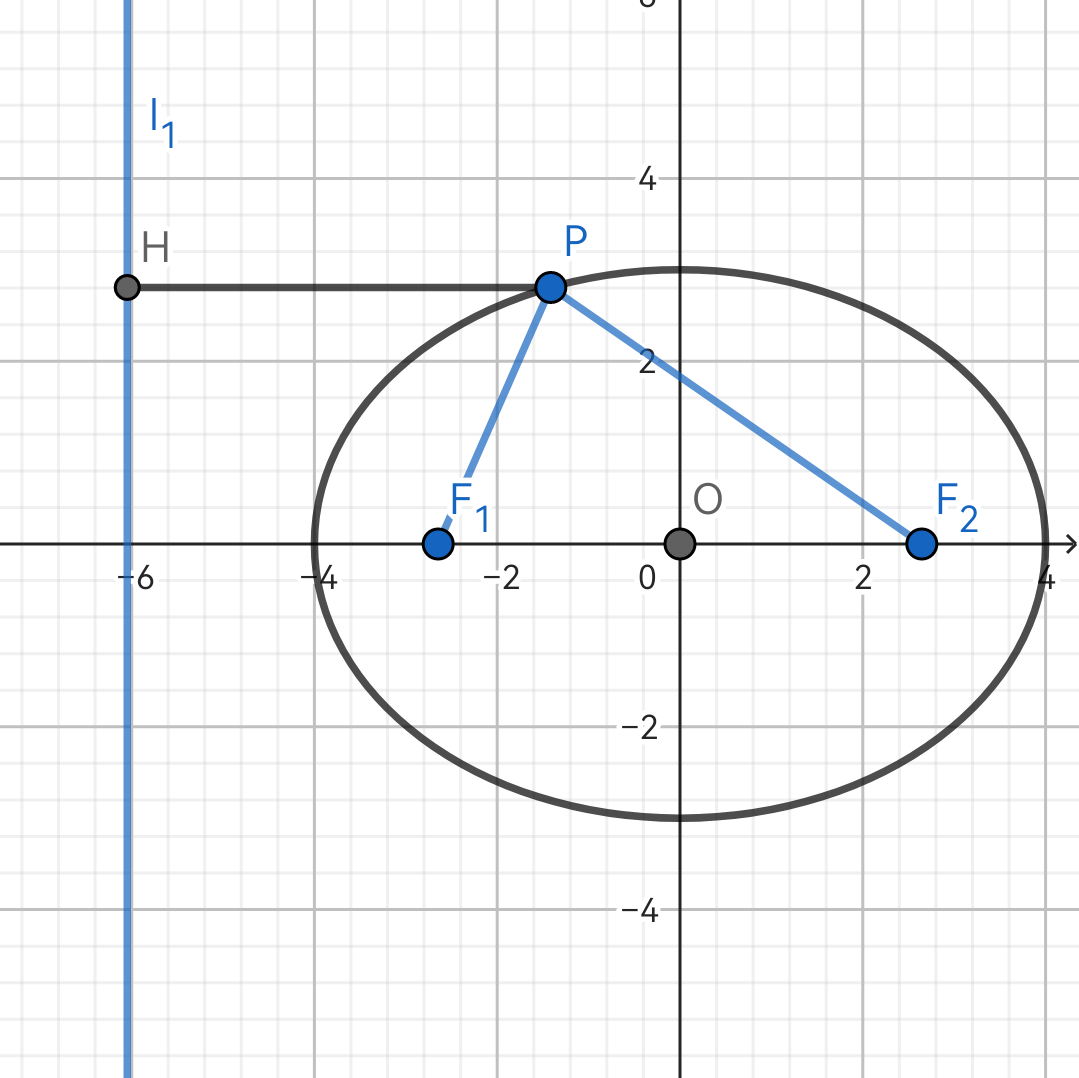
Fig. 2(a)\text{Fig. 2(a)}

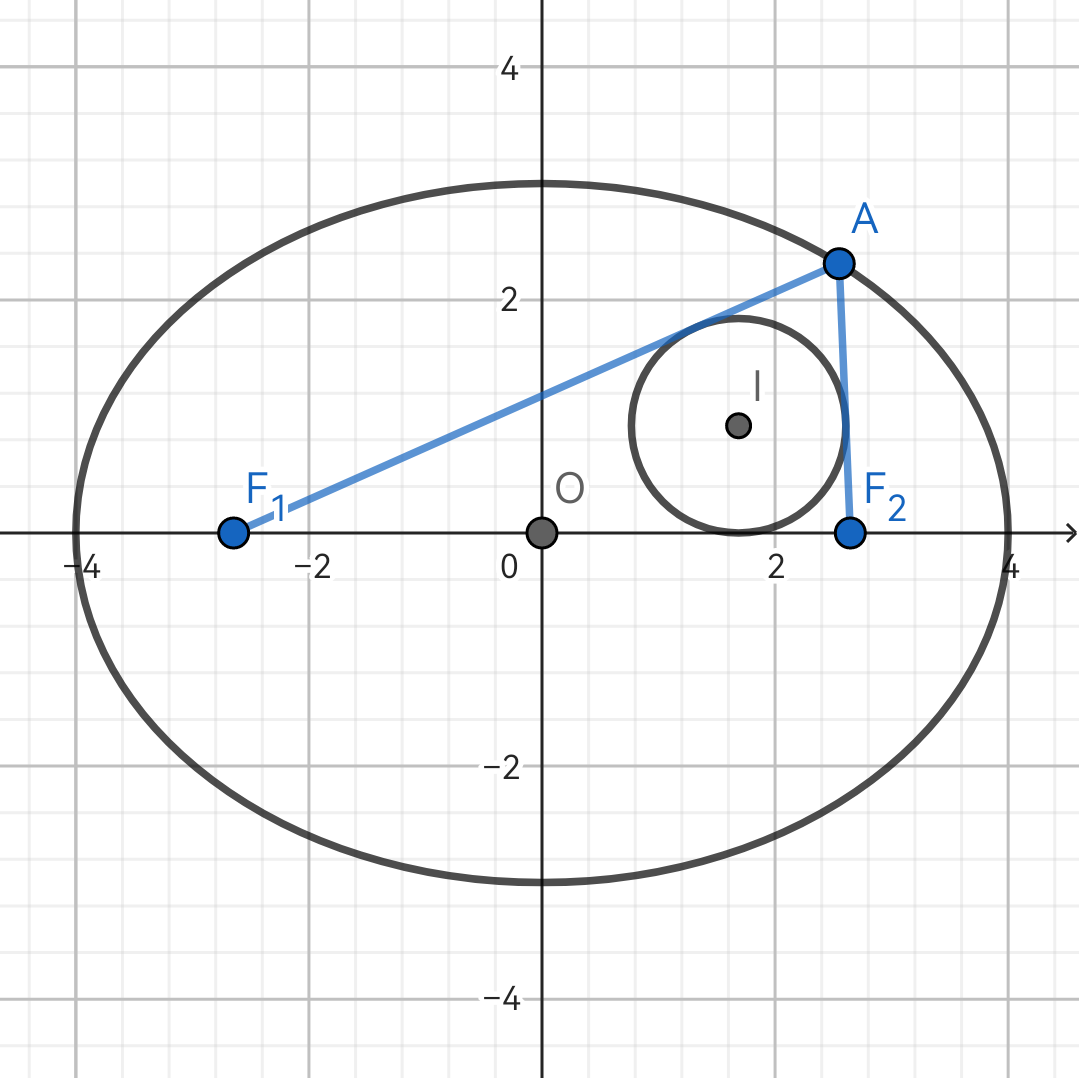
Fig. 2(b)\text{Fig. 2(b)}

2.1(a)  \bold{2.1}\text{(a)}\space\space PP 为椭圆上一点，PP 到 l1l_1 的距离为 ∣PH∣=d1|PH|=d_1，则有 ∣PF1∣d1=e,∣PF1∣=ed1.\cfrac{|PF_1|}{d_1}=e,|PF_1|=ed_1.

2.2(a)  \bold{2.2}\text{(a)}\space\space 焦半径公式 设 P(x0,y0)P(x_0,y_0) 为椭圆上一点，则有 ∣PF1∣=a−ex0|PF_1|=a-ex_0，∣PF2∣=a+ex0.|PF_2|=a+ex_0.

2.3(b)  \bold{2.3}\text{(b)}\space\space 设 P(x0,y0)P(x_0,y_0) 为椭圆上一点，则 △PF1F2\triangle PF_1F_2 的内心 II 的横坐标 xI=ex0.x_I=ex_0.

焦点弦​

过焦点的直线交椭圆于 A,BA,B 两点，则 ABAB 就称为焦点弦。下面以过右焦点的焦点弦为例。

Fig. 3\text{Fig. 3}

3.1  \bold{3.1}\space\space 若 ∣AF2∣∣BF2∣=λ (λ≥1)\cfrac{|AF_2|}{|BF_2|}=\lambda\space(\lambda\ge1)，ABAB 与 xx 轴的夹角为 θ\theta，则 ∣cos⁡θ∣=λ−1λ+1⋅1e.|\cos\theta|=\cfrac{\lambda-1}{\lambda+1}\cdot\cfrac{1}{e}.

3.2  \bold{3.2}\space\space 1∣AF2∣+1∣BF2∣=2ab2.\cfrac{1}{|AF_2|}+\cfrac{1}{|BF_2|}=\cfrac{2a}{b^2}.（可以由 3.33.3 快速证明）

3.3  \bold{3.3}\space\space ∣AF2∣=ep1+ecos⁡θ, ∣BF2∣=ep1−ecos⁡θ.|AF_2|=\cfrac{ep}{1+e\cos\theta},\space|BF_2|=\cfrac{ep}{1-e\cos\theta}. 其中p=b2cp=\cfrac{b^2}{c}，即焦点到准线的长度。

中点弦​

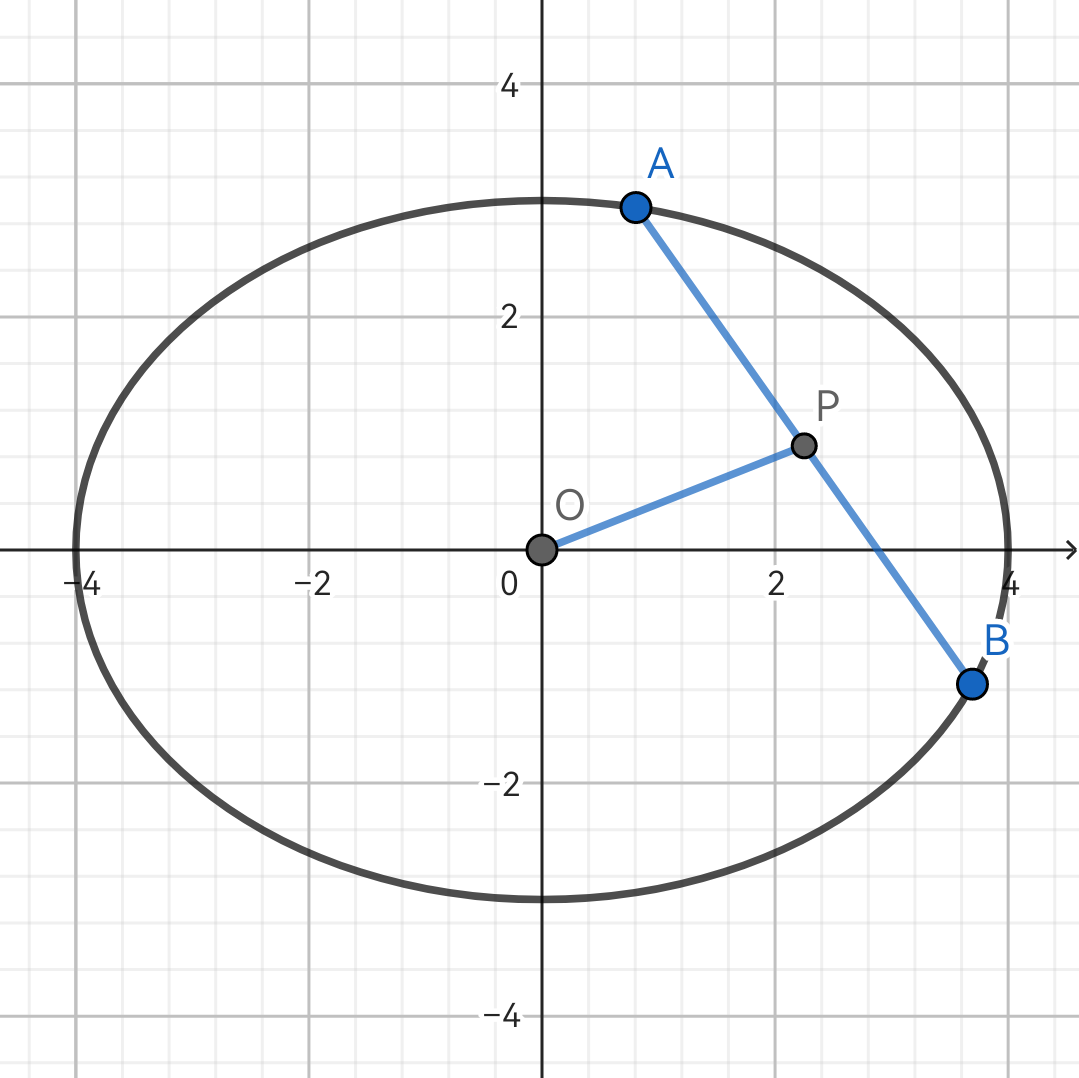
A(x1,y1),B(x2,y2)A(x_1,y_1),B(x_2,y_2) 是椭圆上两点，PP 为 ABAB 中点，这样的模型就称为中点弦模型。

Fig. 4(a)\text{Fig. 4(a)}

Fig. 4(b)\text{Fig. 4(b)}

4.1(a)  \bold{4.1}\text{(a)}\space\space y12−y22x12−x22=−b2a2.\cfrac{y_1^2-y_2^2}{x_1^2-x_2^2}=-\cfrac{b^2}{a^2}.

4.2(a)  \bold{4.2}\text{(a)}\space\space kOP⋅kAB=−b2a2.k_{OP}\cdot k_{AB}=-\cfrac{b^2}{a^2}.（由 4.14.1 推出）

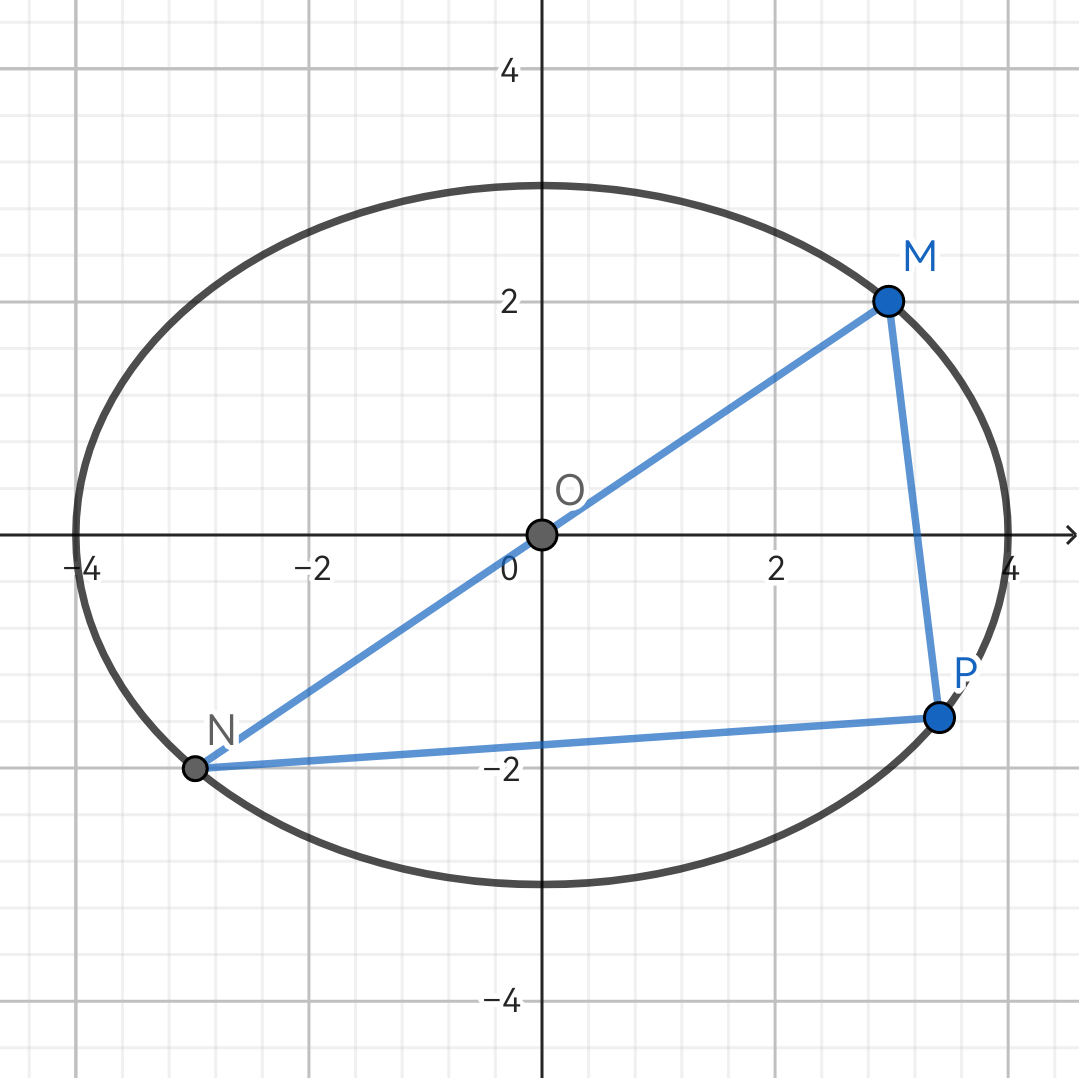
4.3(b)  \bold{4.3}\text{(b)}\space\space 椭圆第三定义 过原点的直线交椭圆于 M,NM,N 两点，PP 为椭圆上一点，则有 kMP⋅kNP=−b2a2.k_{MP}\cdot k_{NP}=-\cfrac{b^2}{a^2}.